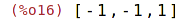Datové typy
1 Seznam (list)
| (%i1) | s:[1,4,25,9,16,25]; |
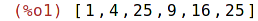
Stejné objekty se mohou vyskytovat více než jednou,
zachovává se zadané uspořádání.
Ověření, že s je datového typu seznam:
| (%i2) | listp(s); |
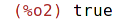
Vytváření seznamu
| (%i3) | makelist(i^2,i,1,5); |
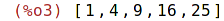
makelist (expr, i, i_0, i_1) vytváří seznam, kde j-tý element je roven
ev (expr, i=j) pro j od i_0 do i_1.
| (%i4) | makelist(x=y,y,[a,b,c]); |
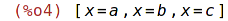
makelist (expr, x, list) vytváří seznam, kde j-tý element je roven
ev (expr, x=list[j]) pro j od 1 do počtu prvků seznamu.
| (%i5) | create_list(x^i,i,[1,3,7]); |
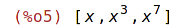
Počet prvků seznamu (délka seznamu):
| (%i6) | length(s); |
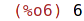
Test, zda daný element patří do seznamu:
| (%i7) | member(2,s); |
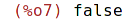
| (%i8) | member(4,s); |
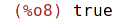
Výběr jednotlivých prvků seznamu:
| (%i9) | s[1]; |

Nahrazení prvku seznamu jiným:
| (%i10) | s[1]:a; |

| (%i11) | s; |
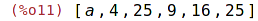
| (%i12) | first(s);second(s);third(s);fourth(s);fifth(s); |

| (%i17) | last(s); |
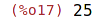
Odstranění elementu ze seznamu:
| (%i18) | delete (y, [w, x, y, z, z, y, x, w]); |
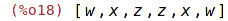
Odstranění duplicit
| (%i19) | seznam:[x, x, x*y, x*(x-1)]; |
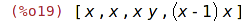
| (%i20) | unique(seznam); |
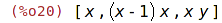
| (%i21) | cl : [black, red, green, yellow, blue, white, pink]; |
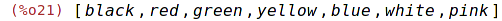
| (%i22) | rest(cl,2); |
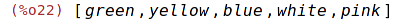
Odstraní první dva prvky seznamu.
| (%i23) | rest(cl,-2); |
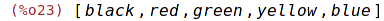
Odstraní poslední dva prvky seznamu.
| (%i24) | rest(cl); |
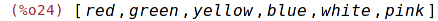
Odstraní první prvek seznamu.
| (%i25) | reverse(cl); |
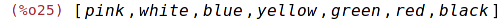
Obrátí pořadí prvků seznamu.
| (%i26) | cons(orange,cl); |
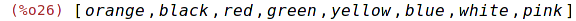
Vytvoří nový seznam se zadaným prvkem na prvním místě.
| (%i27) | endcons(orange,cl); |
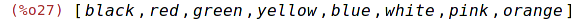
Vytvoří nový seznam se zadaným prvkem na posledním místě.
| (%i28) | append(cl,[orange,brown]); |
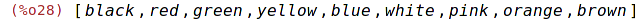
append(list_1,...,list_n) vytváří jeden seznam, skládající se postupně z prvků
seznamu list_1,list_2,...,list_n.
| (%i29) | L1:[1,2,3,4,5]; |
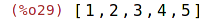
| (%i30) | L2:[a,b,c,d,e]; |
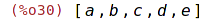
| (%i31) | join(L1,L2); |
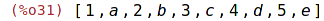
join(l,m) vytváří seznam spojením seznamů l a m, přičemž prvky obou seznamů se
pravidelně střídají. Tj. výsledný seznam vypadá takto: [l[1], m[1], l[2], m[2],...].
Pokud mají oba seznamy různou délku, join ignoruje prvky delšího seznamu.
| (%i32) | f(x):=x^2; |
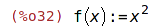
| (%i33) | map(f,L1); |
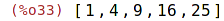
map(f, list) aplikuje funkční předpis na všechny prvky seznamu.
Sečtení prvků seznamu
| (%i34) | apply("+",L1); |

| (%i35) | random(11); |
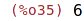
random(x) vrací náhodně zvolené celé číslo od 0 do x-1.
| (%i36) | 3<5, pred; |
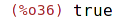
| (%i37) | L : makelist(random(11),i,1,10); |
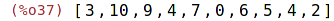
| (%i38) | sublist(L, lambda([x], is(x<5))); |
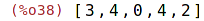
| (%i39) | f(x) := is(x<5)$ |
| (%i40) | f(4); |
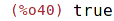
| (%i41) | sublist(L,f); |
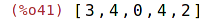
| (%i42) | sublist(L, evenp); |
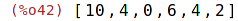
2 Množina (set)
| (%i43) | M1:set(b,a,c); |
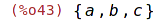
| (%i44) | M1:{c,b,a}; |
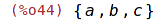
Pokud množina obsahuje stejné prvky, jsou automaticky odstraněny.
Datový typ množina používá vnitřní systém uspořádání.
| (%i45) | setp(M1); |
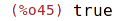
Prázdná množina:
| (%i46) | set(); |
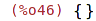
| (%i47) | subst(c=a, M1); |
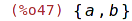
| (%i48) | M2:set(1,2,3); |
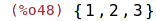
| (%i49) | M3:[1,1,2,2,3,3]; |
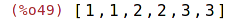
Vytvoření množiny ze seznamu:
| (%i50) | M4:setify(M3); |
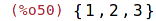
A zpětné vytvoření seznamu z množiny:
| (%i51) | listify(M4); |
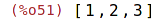
| (%i52) | full_listify ({a, b, {c, {d, e, f}, g}}); |
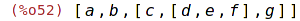
| (%i53) | listify ({a, b, {c, {d, e, f}, g}}); |
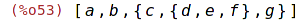
| (%i54) | fullsetify ([a, [a]]); |
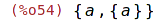
Základní množinové operace
Sjednocení:
| (%i55) | union(M1,M2); |
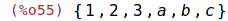
Průnik:
| (%i56) | intersect(M1,M2); |
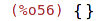
Rozdíl:
| (%i57) | setdifference({0,1,2,3},{0,2,4,6}); |
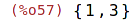
Počet prvků konečné množiny:
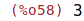
| (%i58) | cardinality(M1); |
| (%i59) | s:{1,2,five,3,4}; |
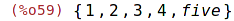
Přidání prvku:
| (%i60) | adjoin(x, s); |
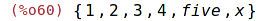
| (%i61) | union(s,{x}); |
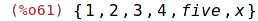
Odstranění prvku z množiny:
| (%i62) | disjoin(x,%); |
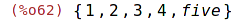
| (%i63) | disjointp ({a, b, c}, {1, 2, 3}); |
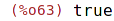
disjoint vrací true, pokud jsou zadané množiny disjunktní.
| (%i64) | disjointp ({a, b, 3}, {1, 2, 3}); |
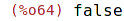
Určuje, zda daný prvek patří do množiny:
| (%i65) | elementp(1,s); |
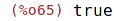
| (%i66) | elementp(6,s); |
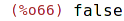
Určuje, zad jsou zadané množiny totožné:
| (%i67) | setequalp ({1, 2, 3}, {1, 2, 3}); |
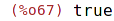
| (%i68) | setequalp ({a, b, c}, {1, 2, 3}); |
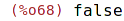
| (%i69) | subset ({1, 2, 7, 8, 9, 14}, evenp); |
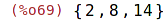
Vytvoří podmnožinu dané množiny na základě zadaného kritéria.
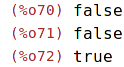
| (%i70) | evenp(1);evenp(1/2);evenp(2); |
| (%i73) | oddp(1);oddp(1/2);oddp(2); |
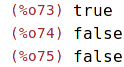
Určuje, zda je první zadaná množina podmnožinou druhé.
| (%i76) | subsetp ({1, 2, 3}, {a, 1, b, 2, c, 3}); |
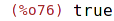
| (%i77) | subsetp ({a, 1, b, 2, c, 3}, {1, 2, 3}); |
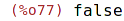
Vrací množinu všech podmnožin zadané množiny:
| (%i78) | collection:powerset({1,2,3}); |
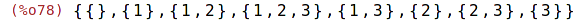
| (%i79) | cardinality(collection); |

| (%i80) | fourth(collection); |
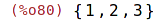
| (%i81) | numbers:{0,%pi,%pi/3,%pi/2}; |
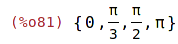
| (%i82) | map(g,numbers); |
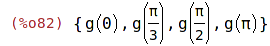
| (%i83) | map(sin, numbers); |
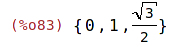
3 Pole (array)
array (name, dim_1, ..., dim_n) vytváří obecné pole.
n musí být menší nebo rovné pěti.
| (%i84) | array(A,2,3); |

| (%i85) | A[1,1]:1;A[1,2]:4;A[1,3]:9; |

| (%i88) | A[2,1]:1;A[2,2]:8;A[2,3]:27; |

| (%i91) | arrayinfo(A); |
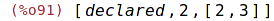
| (%i92) | listarray (A); |
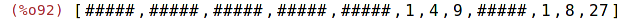
| (%i93) | translate:[["jedna", 1], ["dve", 2], ["tri",3]]; |
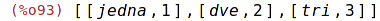
| (%i94) | assoc("jedna", translate); |

| (%i95) | cons(["ctyri",4], translate); |
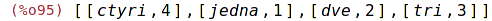
4 Matice
K vytvoření matice použijeme příkaz matrix([],[],...), přičemž v hranatých
závorkách vypisujeme jednotlivé řádky matice.
| (%i96) | D:matrix([1,2,3],[1,4,9],[1,8,27]); |

| (%i97) | D[1,1]; |

Definování indexační funkce
| (%i98) | h[i,j]:=1/(i+j-x); |
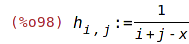
| (%i99) | hilbert4 : genmatrix(h,4,4); |
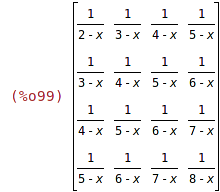
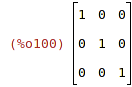
| (%i100) | ident(3); |
| (%i101) | diagmatrix(3,0); |

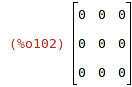
| (%i102) | zeromatrix(3,3); |
Operace s maticemi
| (%i103) | A: matrix([2,a], [-1,-2*b]); |
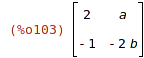
| (%i104) | B : matrix([3*a,2], [1-b,1]); |
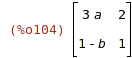
Sečítání a odečítání matic
| (%i105) | A+B; |
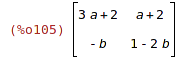
| (%i106) | A-B; |
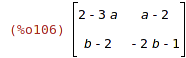
| (%i107) | C:transpose(D); |

Násobení matic
| (%i108) | D.C; |

| (%i109) | expand(A.B); |
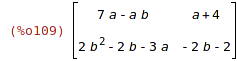
| (%i110) | A*B; |
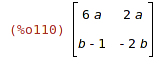
Při použití * se pouze vynásobí prvky na odpovídajících pozicích.
| (%i111) | A/B; |
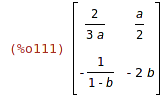
Dělí prvky na odpovídajících pozicích.
Mocniny
| (%i112) | B^^3; |
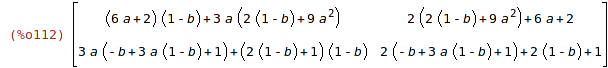
| (%i113) | B^3; |
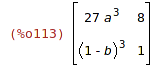
Operátor "^" umocní jen prvky na odpovídajícíh pozicích.
Počet řádků
| (%i114) | length(D); |
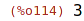
Počet sloupců
| (%i115) | length(transpose(D)); |

Hodnost matice
| (%i116) | rank(D); |

Výpočet determinaru čtvercové matice:
| (%i117) | determinant(D); |
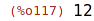
| (%i118) | invert(D); |

| (%i119) | D.%; |

| (%i120) | kill(all); |
Gaussova eliminace
| (%i1) | A:matrix([1,1,3,-3],[5,5,13,-17],[3,1,7,-11]); |
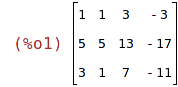
| (%i2) | triangularize(A); |
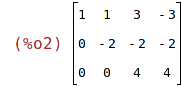
| (%i3) | echelon(A); |

| (%i4) | load("/home_zam/plch/vyuka/maxima/rref.mac"); |

| (%i5) | rref(A); |

Balíček linearalgebra
| (%i6) | load(linearalgebra); |
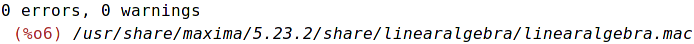
| (%i7) | toeplitz([1,2,3]); |
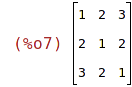
| (%i8) | toeplitz([alpha, beta]); |
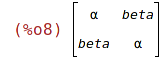
Pro práci s vektory slouží balíček vect
| (%i9) | load(vect); |

| (%i10) | v1 : [1,0,1]; |
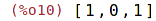
| (%i11) | length(v1); |

| (%i12) | v2 : [0,1,1]; |
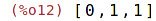
| (%i13) | v1-v2; |
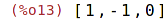
Skalární součin
| (%i14) | v1 . v2; |
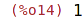
Vektorový součin
| (%i15) | v1 ~ v2; |
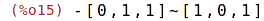
zde nedochází automaticky k vyhodnocení, to provedeme až pomocí
| (%i16) | express(%); |