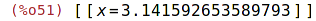Funkce, řešení rovnic
1 Funkce
Pro definování funkcí používáme operátor :=.
| (%i1) | f(x):=x^2; |
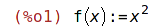
| (%i2) | f(2);f(y); |

Vypsání seznamu uživatelem definovaných funkcí
| (%i4) | functions; |
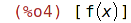
Vypsání definice uživatelem definované funkce
| (%i5) | fundef(f); |
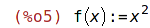
Ekvivalentní způsob zápisu pomocí define
| (%i6) | define(g(x), x^3); |
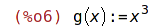
| (%i7) | g(3); |
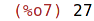
| (%i8) | functions; |
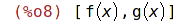
| (%i9) | solve(f(x)=9,x); |
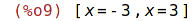
Rozdíl mezi operatorem := a funkcí define
| (%i10) | f1(x):=print(x)$ |
| (%i11) | define(f2(x), print(x))$ |
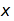
V případě ":=" zůstávají obě strany nevyhodnoceny. V případě použití define je pravá
strana vyhodnocena.
| (%i12) | fundef(f1); |
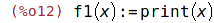
| (%i13) | fundef(f2); |
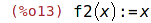
| (%i14) | f1(5); |

| (%i15) | f2(5); |
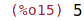
| (%i16) | f(x):=x^3; |
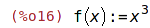
| (%i17) | fp(x):=diff(f(x),x); |
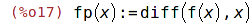
| (%i18) | fp(1); |

Chybové hlášení je vyvoláno operací diff(f(1),1), nejdříve se provede substituce
hodnoty za proměnnou a teprve poté výpočet derivace.
| (%i19) | define(fd(x), diff(f(x), x)); |
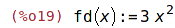
| (%i20) | fd(1); |

Funkce více proměnných
| (%i21) | f(x,y):=x^3-3*x*y^2; |
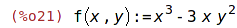
| (%i22) | f(3,2); |
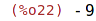
Definování funkce jako posloupnosti výrazů
| (%i23) | f(x):= (a: x^2+4, b: x^3+3*x, 2/a+b/a+b^2); |
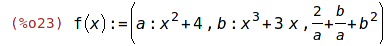
| (%i24) | f(t); |
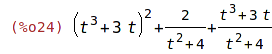
| (%i25) | f(2); |
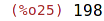
| (%i26) | f(x):= (a: x^2+4, b: x^3+3*x, ratsimp(2/a+b/a+b^2)); |
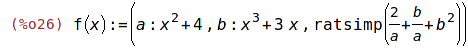
| (%i27) | f(t); |
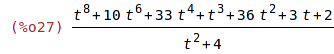
| (%i28) | unit_step(1);unit_step(0);unit_step(-1); |
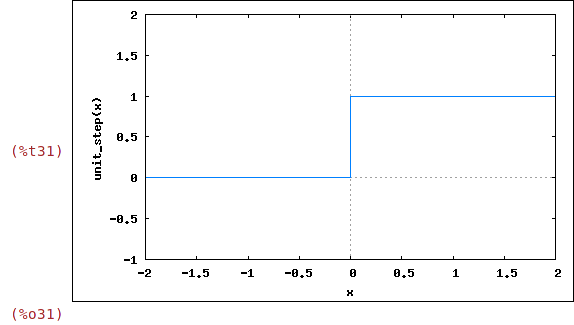
| (%i31) | wxplot2d(unit_step(x),[x,-2,2],[y,-1,2]); |
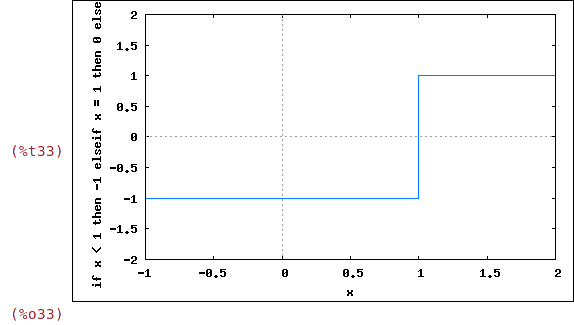
Definování po částech spojité funkce
| (%i32) | f1(x):=(if x<1 then -1 elseif x=1 then 0 else 1); |
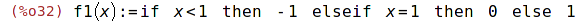
| (%i33) | wxplot2d(f1(x),[x,-1,2],[y,-2,2]); |
| (%i34) | f1(%pi); |

| (%i35) | sgn(n):=(if integerp(n)=true then (-1)^n else print(n, "neni integer")); |
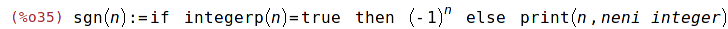
| (%i36) | sgn(%pi); |

| (%i37) | sgn(4); |
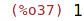
Rekurzivní definice
| (%i38) | L(n):=(if n=1 then 1 elseif n=2 then 3 else L(n-1)+L(n-2))$ |
| (%i39) | L(20); |
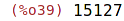
| (%i40) | trace(L); |
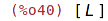
| (%i41) | L(4); |

| (%i42) | untrace(L); |
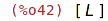
| (%i43) | L[n]:=(if n=1 then 1 elseif n=2 then 3 else L[n-1]+L[n-2])$ |
| (%i44) | L[20]; |
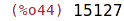
| (%i45) | arrays; |
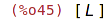
| (%i46) | arrayinfo(L); |

| (%i47) | showtime:true$ |
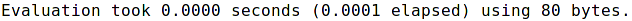
| (%i48) | L(21); |
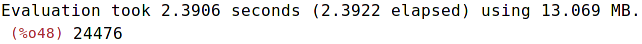
| (%i49) | L[21]; |
| (%i50) | showtime:false$ |
Spočtené hodnoty jsou ukládány do pole a v případě potřeby nejsou opětně počítány.
Pro výpočet L[21] je tedy potřeba jen jeden krok.
| (%i51) | kill(all); |
Vytvoření funkce z výrazu
| (%i1) | vzorec:(b^2*x^2*sin(b*x)-2*sin(b*x)+2*b*x*cos(b*x)*a*t)/b^3; |
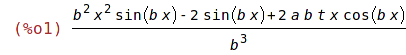
| (%i2) | define(F(x,t), vzorec); |
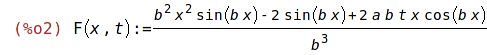
| (%i3) | F(0,1);F(%pi/b,5); |
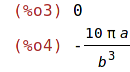
Operace s funkcemi
| (%i5) | f(x):=log(x)+1;g(y):=exp(y)-1; |
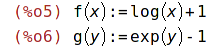
| (%i7) | f(z)+g(z); |
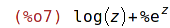
| (%i8) | f(z)*g(z); |
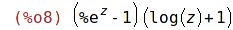
| (%i9) | f(g(z)); |
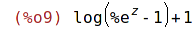
| (%i10) | g(f(z)); |
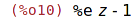
Použití anonymní funkce
| (%i11) | kill(all); |
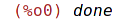
| (%i1) | functions; |
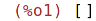
| (%i2) | f : lambda([x], x^2); |
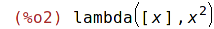
| (%i3) | f(a); |

| (%i4) | f(2); |

| (%i5) | functions; |
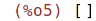
| (%i6) | map(f, a+b+c); |
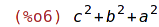
| (%i7) | map(lambda([x], x^2), a+b+c); |
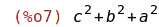
| (%i8) | map(lambda([x], x^2), [1,2,3]); |
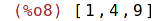
2 Rovnice
| (%i9) | eqn:(x-1)*(x^2+x+1); |
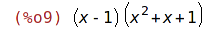
| (%i10) | sol:solve(eqn,x); |
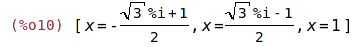
Pokud rovnice obsahuje pouze jednu proměnnou, nemusíme druhý parametr zadávat.
| (%i11) | sol: solve(eqn); |
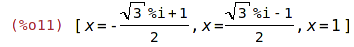
| (%i12) | sol[1];sol[2]; |
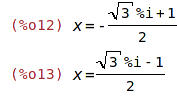
| (%i14) | ev(expand(eqn), sol[1]);ev(expand(eqn), sol[2]); |

| (%i16) | rov: x^3 - 4*x^2 + 6*x - 4 = 0; |
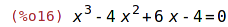
| (%i17) | solve(rov); |
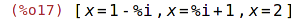
Pouze reálná řešení
| (%i18) | algsys([rov],[x]), realonly:true; |
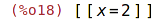
Rovnice s parametrem
| (%i19) | eqn:x^3+2*a*x^2+a*x=1; |
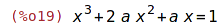
| (%i20) | solve(eqn,x); |
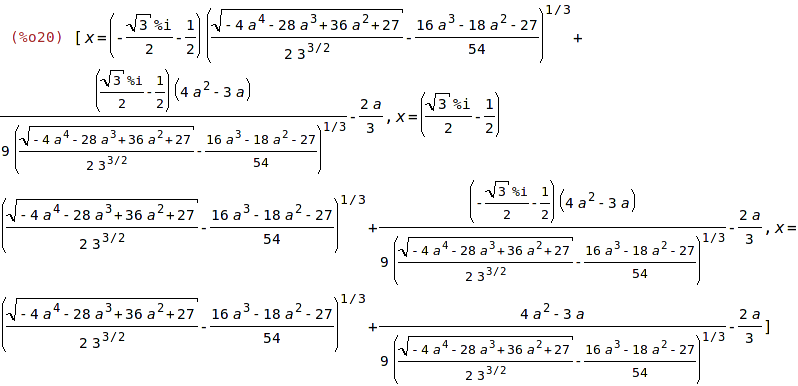
Řešení nerovnic
| (%i21) | load(solve_rat_ineq); |
| (%i22) | solve_rat_ineq(x^3+4*x^2+2*x-1>0); |
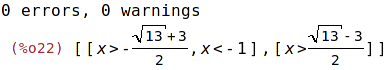
Soustavy rovnic
| (%i23) | s:solve([x+2*y=3, y+1/x=1], [x,y]); |
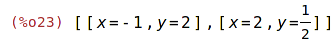
| (%i24) | ev([x+2*y=3, y+1/x=1],s[1]); |
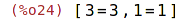
| (%i25) | solve([y^2+1=x,x+2=y], [x,y]); |
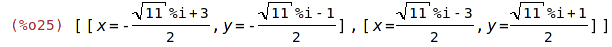
Příkaz linsolve slouží k řešení lineárních rovnic a jejich soustav
| (%i26) | linsolve([y+x=1,x-2=3],[y,x]); |
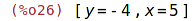
| (%i27) | solve(sin(x)=1/2,x); |

| (%i28) | eqn :product(x-k,k,1,110); |
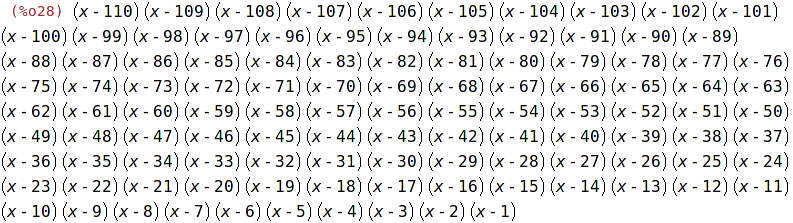
| (%i29) | solve(eqn,x); |
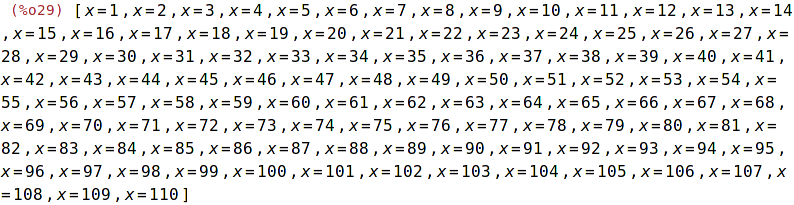
| (%i30) | eqn:x+x^(1/3)=-2; |
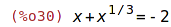
| (%i31) | solve(eqn, x); |
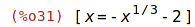
Příliš mnoho řešení
| (%i32) | eqn :sin(x)^3 -13/2*sin(x)^2 + 11*sin(x) = 4; |
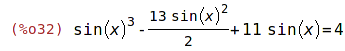
| (%i33) | solve(eqn,x); |

| (%i34) | solve(eqn,sin(x)); |

| (%i35) | solve(sin(x)=1/2,x); |

| (%i36) | r1:(x-1)^2/(x^2-1)=0; |
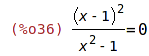
| (%i37) | solve(r1,x); |
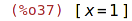
| (%i38) | ev(r1,x=1); |

Numerické řešení
| (%i39) | r:x^7-2*x^6-4*x^5-x^3+x^2+6*x+4; |
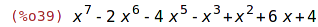
| (%i40) | solve(r); |
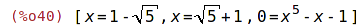
| (%i41) | if numer#false then numer:false else numer:true; |
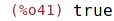
| (%i42) | solve(r); |
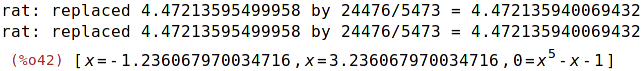
Příkaz find_root slouží pro numerické řešení rovnic. První dva parametry jsou stejné
jako u příkazu solve, druhé dva určují krajní body intervalu, na kterém rovnici řešíme.
| (%i43) | find_root(r,x,-2,0); |
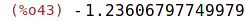
| (%i44) | find_root(r,x,0,2); |
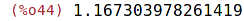
| (%i45) | find_root(r,x,2,4); |

| (%i46) | allroots(r); |

| (%i47) | realroots(r); |
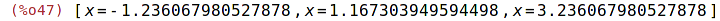
| (%i48) | load(mnewton); |
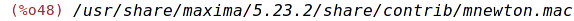
| (%i49) | mnewton(r,x,2); |
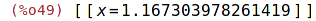
| (%i50) | mnewton(sin(x),x,0); |
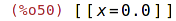
| (%i51) | mnewton(sin(x),x,3); |