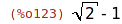Polynomy a racionální funkce

1 Polynomy

(%i16) p1:-3*x+7*x^2-3*x^3+7*x^4;

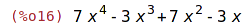
Result

(%i17) polynomialp(p1,[x]);

Result

(%i18) coeff(p1,x,4);

Result

(%i19) coeff(p1,x);

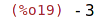
Result

(%i20) load(powers)$

Result

(%i21) powers(p1,x);

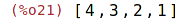
Result

1.1 Sčítání a násobení polynomů

(%i22) p2:5*x^5+3*x^3+x^2-2*x+1;

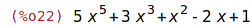
Result

(%i23) 2*p1-3*p2+3;

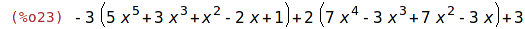
Result

(%i24) expand(%);

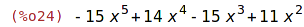
Result

(%i25) 2*p1-3*p2+3, expand;

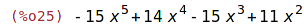
Result

(%i26) p1*p2;

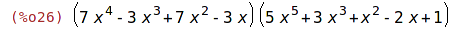
Result

(%i27) expand(%);

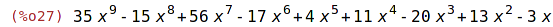
Result

Maxima neprovádí roznásobení automaticky.

(%i28) (3*x+5)^10;

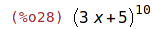
Result

(%i29) expand(%);

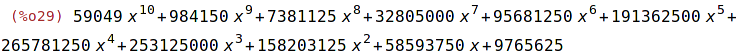
Result

(%i30) expr:(x+1)^2*(y+1)^3;

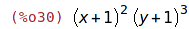
Result

(%i31) expand(expr);

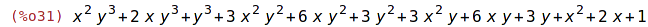
Result

(%i32) expand(expr,2);

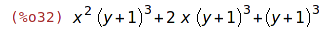
Result

(%i33) expr:(x+1)^-2*(y+1)^3;

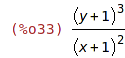
Result

expand(expr,p,n) provede roznásobení jen u členů, jejichž mocniny jsou od -n do p.

(%i34) expand(expr,2,2);

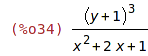
Result

Členy polynomu jsou automaticky setříděny sestupně vzhledem ke stupni.

1.2 Dělení se zbytkem, největší společný dělitel

(%i35) q : quotient(p2,p1);

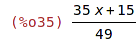
Result

(%i36) r : remainder(p2,p1);

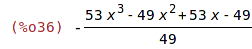
Result

(%i37) is (p2=expand(q*p1+r));

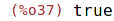
Result

(%i38) divide(p2,p1);

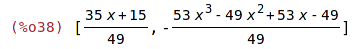
Result

(%i39) gcd(p2,p1);

Result

(%i40) pol:expand(p2*p1);

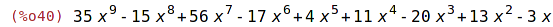
Result

(%i41) factor(pol);

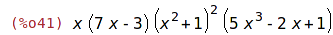
Result

gfactor pracuje s oborem komplexních čísel

(%i42) gfactor(pol);

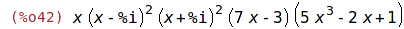
Result

(%i43) p:x^2+1;

Result

(%i44) factor(p);

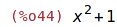
Result

(%i45) gfactor(p);

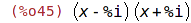
Result

(%i46) pol:8*x^3-12*x;

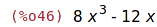
Result

(%i47) factor(pol);

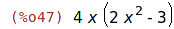
Result

(%i48) grind;

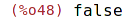
Result

1.3 Polynomy více proměnných

(%i49) pol:6*x*y^5+12*y^4+14*y^3*x^3 -15*x^2*y^3 + 9*x^3*y^2 - 30*x*y^2 -
35*x^4*y + 18*y*x^2 +21*x^5;

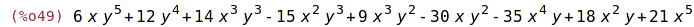
Result

(%i50) ordergreat(x,y);

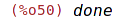
Result

(%i51) 6*x*y^5+12*y^4+14*y^3*x^3 -15*x^2*y^3 + 9*x^3*y^2 - 30*x*y^2 -
35*x^4*y + 18*y*x^2 +21*x^5;

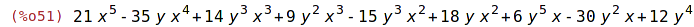
Result

(%i52) unorder();

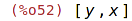
Result

(%i53) factor(pol);

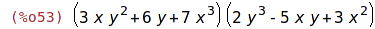
Result

(%i54) collectterms(pol, x);

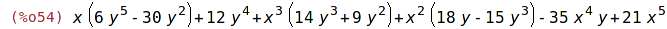
Result

(%i55) collectterms(pol,y);

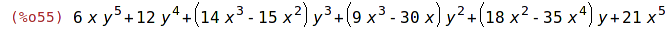
Result

2 Racionální funkce

(%i56) r:(x^2+3*x+2)/ (x^2+5*x+6);

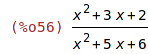
Result

Maxima neprovádí zjednodušení automaticky.

(%i57) num(r);denom(r);

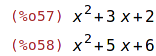
Result

(%i59) rat(r);

Result

(%i60) (x^(100)-1)/(x-1);

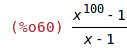
Result

(%i61) rat(%);

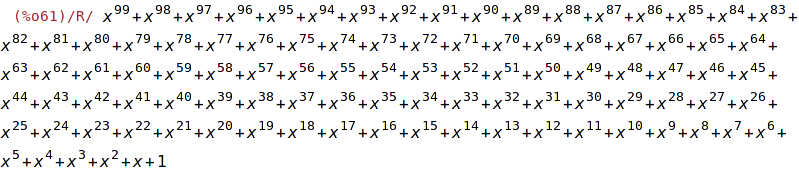
Result

(%i62) f:161*y^3+333*x*y^2+184*y^2+162*x^2*y+144*x*y+77*y+99*x+88$

(%i63) g:49*y^2+28*x^2*y+63*x*y+147*y+36*x^3+32*x^2+117*x+104$

(%i64) racfce:f/g;

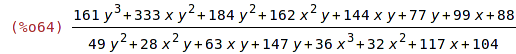
Result

(%i65) rat(racfce);

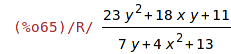
Result

Rozklad na parciální zlomky.

(%i66) q:(x^3+x^2-x+1)/p1;

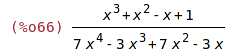
Result

(%i67) partfrac(q, x);

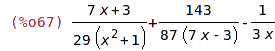
Result

(%i68) 1/(x^4-5*x^2+6);

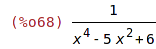
Result

(%i69) partfrac(%, x);

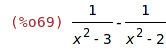
Result

2.1 Příklady na manipulaci s racionálními funkcemi

(%i70) power:(x+1)^(-2);

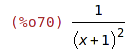
Result

(%i71) expand(power);

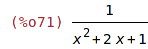
Result

Narozdíl od Maplu se expandují í záporné mocniny.

(%i72) r1:(x+1)^2/((x^2+x)*x);

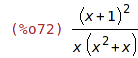
Result

(%i73) expand(r1);

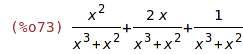
Result

(%i74) r2:expand(num(r1))/expand(denom(r1));

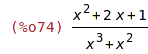
Result

(%i75) factor(r2);

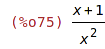
Result

(%i76) (x-1)*(x+2)/((x+1)*x)+(x-1)/(1+x)^2;

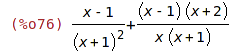
Result

(%i77) rat(%);

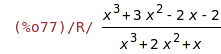
Result

Expand použité na racionální funkci ji převede na součet zlomků.

(%i78) expand((x^2+2*x+2)/(x^2-2*x+2));

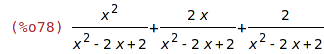
Result

(%i79) ratsimp(%);

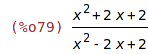
Result

3 Zjednodušování výrazů

Příkazy rat, ratsimp a radcan slouží ke zjednodušování výrazů.

(%i80) x+y/(x+2)+ z/(x^2+4);

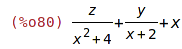
Result

Příkaz ratsimp aplikovaný na součet zlomků provede převod na společného
jmenovatele.

(%i81) ratsimp(%);

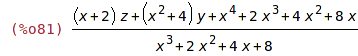
Result

Při aplikaci na polynom upraví polynom do tzv. "collected form".

(%i82) ratsimp(x*(x+2)+(x-3)*(x+4));

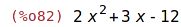
Result

Pro úpravy výrazů s obecnými exponenty, logaritmy a odmocninami používámé příkaz radcan.

(%i83) expr : (exp(x)-1)/(exp(x/2)+1);

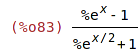
Result

(%i84) %, ratsimp;

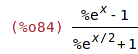
Result

(%i85) %, radcan;

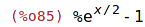
Result

(%i86) logexpr : log((x+2)*(x-2)) + log(x);

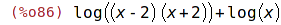
Result

(%i87) logexpr, ratsimp;

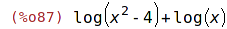
Result

(%i88) logexpr, radcan;

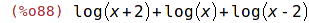
Result

(%i89) %, logcontract;

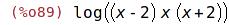
Result

(%i90) logexpr, logcontract;

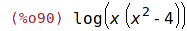
Result

(%i91) (log(x+x^2)-log(x))^n/(log(1+x)^(n/2));

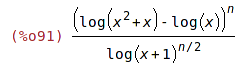
Result

(%i92) radcan(%);

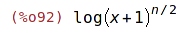
Result

Úpravy výrazů s odmocninami

(%i93) sqrt(2)*sqrt(3), expand;

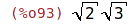
Result

(%i94) sqrt(2)*sqrt(3), radcan;

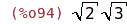
Result

(%i95) sqrt(2)*sqrt(3), rootscontract;

Result

(%i96) sqrt(6)*sqrt(3);

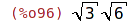
Result

(%i97) sqrt(6)*sqrt(3), radcan;

Result

(%i98) sqrt(6)/sqrt(3);

Result

(%i99) sqrt(6)/sqrt(3), radcan;

Result

Systémová proměnná radexpand může být nastavena na hodnotu true (implicitní nastavení),
all nebo false. Nastavení určuje způsob automatického zjednodušování výrazů s odmocninami.

V implictním případě se sqrt(x^2) zjednoduší na abs(x). Maxima implicitně pracuje
se všemi symboly jako s reálnými čísly. To můžeme změnit nastavením proměnné domain
na hodnotu complex.

(%i100) sqrt(x^2);

Result

(%i101) domain : complex$

(%i102) sqrt(x^2);

Result

(%i103) domain : real$

(%i104) radexpand;

Result

(%i105) sqrt(16*x^2);

Result

(%i106) radexpand: all$

(%i107) sqrt(16*x^2);

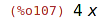
Result

(%i108) radexpand : false;

Result

(%i109) sqrt(16*x^2);

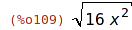
Result

(%i110) (x+2*sqrt(x)+1)/(1+sqrt(x));

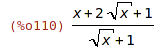
Result

(%i111) radcan(%);

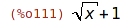
Result

3.1 Úpravy výrazů s goniometrickými funkcemi

(%i112) trigsimp(tan(x));

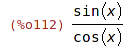
Result

(%i113) sin(x+y), trigexpand;

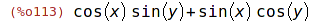
Result

(%i114) x + 3*cos(x)^2 - sin(x)^2, trigreduce;

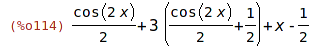
Result

(%i115) trigrat(sin(3*a)/sin(a+%pi/3));

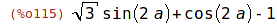
Result

(%i116) rtt(e):= radcan (trigrat (trigsimp (e)));

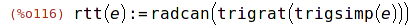
Result

Manuál programu Maxima doporučuje při zjednodušování výrazů s goniometrickými
funkcemi postupně aplikovat příkazy trigreduce, ratsimp a radcan.

(%i117) e : sin(x+y), trigexpand;

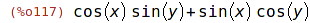
Result

(%i118) rtt(e);

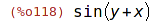
Result

(%i119) e : tan(x+y), trigexpand;

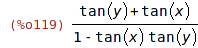
Result

(%i120) rtt(e);

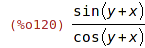
Result

(%i121) tan(%pi/8);

Result

(%i122) load(spangl);

Result

(%i123) tan(%pi/8);

Result

Created with wxMaxima.