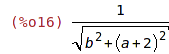Číselné obory
1 Celá čísla
| (%i1) | 1; |
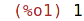
| (%i2) | integerp (1); |
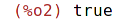
| (%i3) | 4^(4^4); |
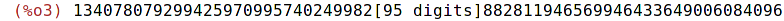
| (%i4) | 2^32-1; |
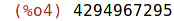
| (%i5) | 4*(2^17-2)-1; |
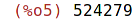
| (%i6) | number:10^29-10^14-1; |
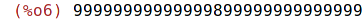
| (%i7) | 123456789^987654321; |

Ověřuje, zda je zadané číslo prvočíslem.
| (%i8) | primep(216091); |
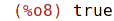
| (%i9) | primep(number); |
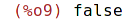
Rozklad na součin prvočísel.
| (%i10) | factor(number); |
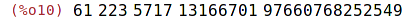
Algoritmus pro rozklad na součin není v Maximě příliš efektivní. Často
je výhodnější použít specializovaný software, např. PARI/GP.
Nejbližší větší a menší prvočíslo.
| (%i11) | next_prime (number); |
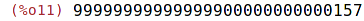
| (%i12) | prev_prime (number); |
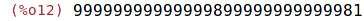
Dělení se zbytkem
| (%i13) |
a:1234$ b:56$ |
| (%i15) | q:quotient(a,b); |
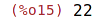
Zbytek po dělení
| (%i16) | r:remainder(a,b); |
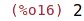
| (%i17) | divide(a,b); |
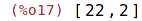
Vypíše podíl i zbytek (ve formě seznamu).
| (%i18) | a=q*b+r; |
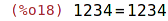
| (%i19) | is(a=q*b+r); |

Největší společný dělitel a nejmenší společný násobek.
| (%i20) | gcd(1234,56); |

| (%i21) | load ("functs"); |
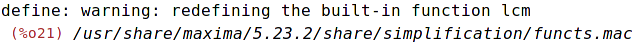
| (%i22) | lcm(21,35,99); |
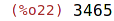
Určení absolutní hodnoty.
| (%i23) | abs(-3); |
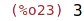
2 Racionální čísla
| (%i24) | 4/6; |

Narozdíl od Maplu může být i jmenovatel záporný.
| (%i25) | -3/-6; |

3 Čísla s pohyblivou desetinnou čárkou
| (%i26) | 25^(1/6); |

| (%i27) | float(%); |
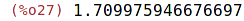
| (%i28) | floatnump(%); |
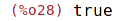
| (%i29) | 1.e-6; |
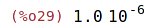
Maxima pracuje standartně s přesností na 16 platných číslic.
Přesnost můžeme změnit nastavením proměnné fpprec, ta se ale projeví
pouze při použití bfloat. fpprec určuje počet platných číslic.
| (%i30) | bfloat(%o25); |
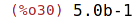
| (%i31) | floatnump(%); |
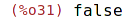
| (%i32) | bfloatp(%o29); |
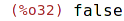
| (%i33) | fpprec; |

| (%i34) | fpprec:30; |

Ludolfovo číslo zadáváme pomocí %pi.
| (%i35) | bfloat (%pi), fpprec=20; |
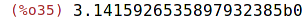
| (%i36) | bfloat (%pi), fpprec=100; |
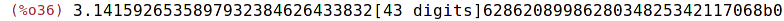
| (%i37) | set_display(ascii); |

| (%i38) | bfloat (%pi), fpprec=100; |

| (%i39) | set_display(xml); |

bfloat používá pro označení exponentu písmeno b.
| (%i40) | 1.b-6; |
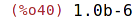
| (%i41) | %pi, numer; |
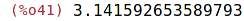
Jakmile zadáme nějaké číslo aproximativně,
Maxima automaticky použije aproximativní aritmetiku.
| (%i42) | 3/2*5; |
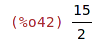
| (%i43) | 3/2*5.0; |
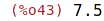
ceiling(x) učuje nejmenší celé číslo větší nebo rovné zadanému x,
floor(x) největší celé číslo menší nebo rovné zadanému x.
| (%i44) | floor(7.5); |
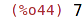
| (%i45) | ceiling(7.5); |
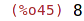
| (%i46) | round(7.5);round(7.4);round(7.6); |

| (%i49) | rationalize(0.5); |

Pomocí příkazů numer:true a numer:false určujeme, zda bude Maxima
používat aritmetiku numerickou nebo symbolickou.
| (%i50) | numer:true; |
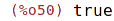
| (%i51) | %pi; |
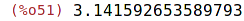
| (%i52) | numer:false; |
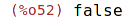
| (%i53) | %pi; |
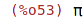
Konstanty:
Eulerovo číslo e
| (%i54) | %e; exp(1); %e, numer; |

Nekonečno, -nekonečno, komplexní nekonečno
| (%i57) | inf; minf; infinity; |

4 Počítání s odmocninami
| (%i60) | (1/2+1/2*sqrt(5))^2; |
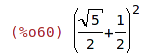
| (%i61) | expand(%); |
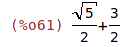
| (%i62) | 1/%; |
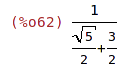
| (%i63) | ratsimp(%); |
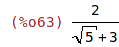
| (%i64) | algebraic:true; |
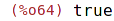
| (%i65) | ratsimp(2/(sqrt(5)+3)); |

Implicitní nastavení je alegebraic : false.
| (%i66) | algebraic : false; |
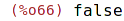
| (%i67) | (-1-3*%pi-3*%pi^2-%pi^3)^(1/3); |
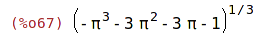
| (%i68) | radcan(%); |
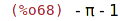
| (%i69) | 1/(1+sqrt(2)); |
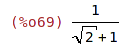
| (%i70) | algebraic : true; |
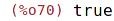
| (%i71) | ratsimp(1/(1+sqrt(2))); |
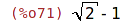
| (%i72) | algebraic : false; |
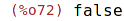
| (%i73) | (4+2*3^(1/2))^(1/2); |
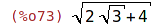
| (%i74) | load(sqdnst); |
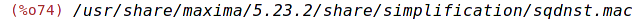
| (%i75) | sqrtdenest((4+2*3^(1/2))^(1/2)); |
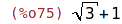
Maxima pracuje standardně v reálném oboru (Maple v komplexním)
| (%i76) | sqrt(x^2); |

| (%i77) | (-8)^(1/3); |
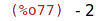
| (%i78) | domain : complex; |
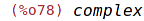
| (%i79) | sqrt(x^2); |

| (%i80) | (-8)^(1/3); |
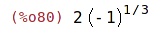
| (%i81) | kill(all); |
5 Komplexní čísla
Komplexní jednotku zadáváme pomocí %i.
| (%i1) | (2+3*%i)*(4+5*%i); |
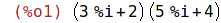
| (%i2) | expand(%); |
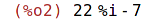
Převod na základní tvar.
| (%i3) | k_cislo : (2+3*%i)/(4+5*%i); |
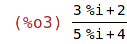
| (%i4) | rectform(%); |
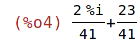
Pro zobrazení reálné, resp. imaginární části komplexního čísla
použijeme příkaz realpart, resp. imagpart.
Komplexní číslo nemusí být v základním tvaru.
| (%i5) | realpart(%);imagpart(%o4); |
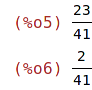
| (%i7) | realpart(k_cislo);imagpart(k_cislo); |
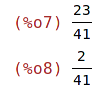
Pro určení čísla komplexně sdruženého použijeme příkaz conjugate
z balíčku eigen.
| (%i9) | load(eigen); |
| (%i10) | conjugate(k_cislo); rectform(%); |

| (%i12) | sqrt(-8); |
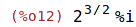
cabs určuje absolutní hodnotu komplexního čísla
| (%i13) | cabs(%); |

| (%i14) | 1/(2+a-b*%i); |
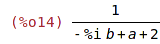
| (%i15) | rectform(%); |
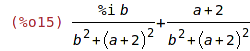
| (%i16) | cabs(1/(2+a-b*%i)); |