Matematická analýza v programu Maxima

1 Symbolické derivování

(%i1) 'diff(exp(-x^2),x);

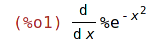
Result

Apostrof před příkazem diff zamezí vyhodnocení. Používá se například pro kontrolu
správnosti zadání.

(%i2) %, nouns;

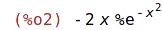
Result

(%i3) 'diff(exp(-x^2),x)$ %=ev(%,nouns);

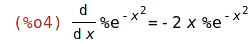
Result

(%i5) 'diff(log(x/(x^2+1)),x)$ %=ev(%,nouns);

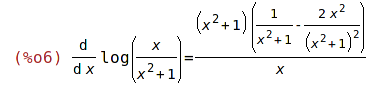
Result

(%i7) rat(%);

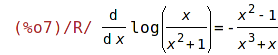
Result

(%i8) 'diff(x^(x^x),x)$ %=ev(%,nouns);

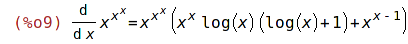
Result

Derivace vyšších řádů:

(%i10) 'diff(exp(-x^2),x,2)$ %=ev(%,nouns);

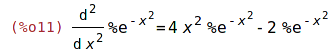
Result

(%i12) 'diff(exp(-x^2),x,5)$ %=ev(%,nouns);

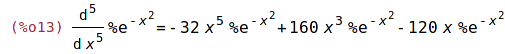
Result

1.1 Derivace funkce dané implicitně

(%i14) eq : x^2 +y^2 = c;

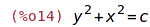
Result

(%i15) depends(y,x);

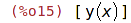
Result

(%i16) diff(eq, x);

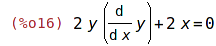
Result

(%i17) dydx : solve(%, 'diff(y,x));

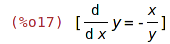
Result

(%i18) dydx : rhs(dydx[1]);

Result

(%i19) diff(eq, x, 2);

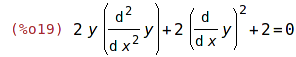
Result

(%i20) solve(%, 'diff(y,x,2));

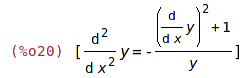
Result

(%i21) rat(subst(dydx, 'diff(y,x,1), %));

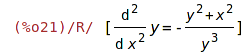
Result

(%i22) remove(y, dependency);

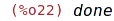
Result

1.2 Parciální derivace

(%i23) 'diff(exp(a*x*y^2),x,1,y,2)$ %=ev(%, nouns);

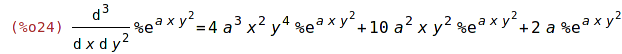
Result

(%i25) factor(%);

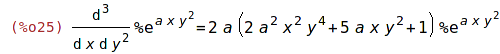
Result

(%i26) 'diff(sin(x+y)/y^4, x,5, y,2)$ %=ev(%, nouns);

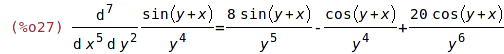
Result

2 Integrace a sumace

2.1 Neurčitý integrál

(%i28) 'integrate(x/(x^3+1),x);

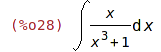
Result

(%i29) 'integrate(x/(x^3+1),x)$ %=ev(%,nouns);

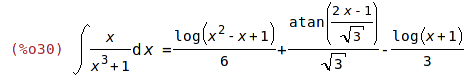
Result

(%i31) diff(rhs(%),x);

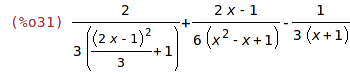
Result

Pomocí rhs() se odkazujeme na pravou stranu zadané rovnice, pomocí lhs()
na levou.

(%i32) rat(%);

Result

(%i33) 'integrate(x/(x^5+1),x)$ %=ev(%,nouns);

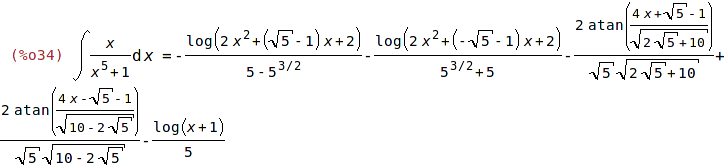
Result

(%i35) radcan(diff(rhs(%),x));

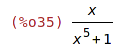
Result

(%i36) 'integrate(2*x*(x^2+1)^24,x)$ %=ev(%,nouns);

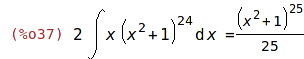
Result

Substituční metoda

(%i38) 'integrate(2*x*(x^2+1)^24,x);

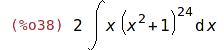
Result

(%i39) changevar(%, x^2+1-t,t,x );

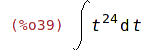
Result

(%i40) ev(%, nouns);

Result

(%i41) subst(t=(x^2+1), %);

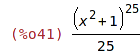
Result

2.2 Určitý integrál

(%i42) 'integrate(x/(x^3+1), x,1,2); %=ev(%, nouns);

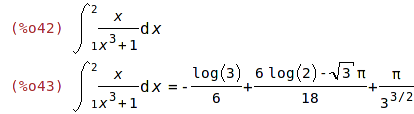
Result

(%i44) 'integrate(1/((1+x^2)*(1+2*x^2)), x,0,1)$ %=ev(%, nouns);

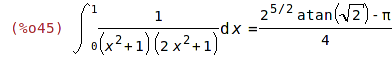
Result

(%i46) integrate(1/x^2, x,-1,1);

Result

Maxima kontroluje nespojitosti integrandu na zadaném intervalu.

(%i47) integrate(t^4*ln(t)^2/(1+3*t^2)^3, t,0,inf);

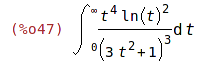
Result

(%i48) 'integrate(exp(asin(x)), x,0,1); %=ev(%, nouns);

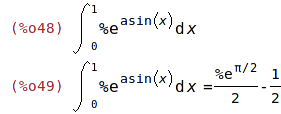
Result

Pozn. Maple tento neurčitý integrál nespočítá.

(%i50) %, numer;

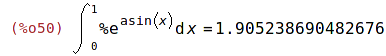
Result

Numerické integrování (Rombergovou metodou)

(%i51) romberg(exp(asin(x)), x,0,1);

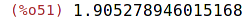
Result

2.3 Konečné a nekonečné součty

(%i52) 'sum(k^7, k,1,20)$ %=ev(%, nouns);

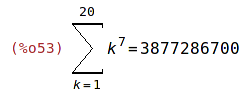
Result

(%i54) 'sum(k^7, k,1,n)$ %=ev(%, nouns, simpsum);

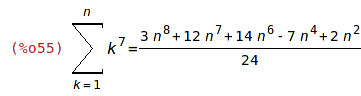
Result

3 Taylorův rozvoj

(%i56) t : taylor(sin(tan(x))-tan(sin(x)),x,0,25);

Result

(%i57) taylorp(t);

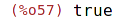
Result

(%i58) taylorinfo(t);

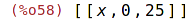
Result

(%i59) sin_series : taylor(sin(x), x,0,5);

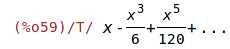
Result

(%i60) subst(x=2, sin_series);

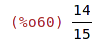
Result

(%i61) diff(sin_series, x);

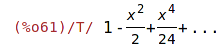
Result

(%i62) integrate(sin_series,x);

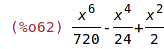
Result

4 Výpočty limit

(%i63) 'limit((x^2-1)/(2*x^2-x-1),x,1)$ %=ev(%, nouns);

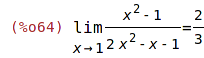
Result

(%i65) 'limit( cos(x)^(1/x^3), x,0)$ %=ev(%, nouns);

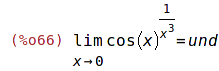
Result

Jednostranné limity

(%i67) 'limit( cos(x)^(1/x^3), x,0, plus)$ %=ev(%, nouns);

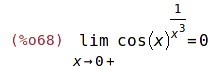
Result

(%i69) 'limit( cos(x)^(1/x^3), x,0, minus)$ %=ev(%, nouns);

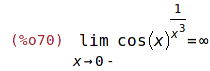
Result

(%i71) y : exp(a*x)*cos(b*x);

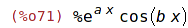
Result

(%i72) 'limit(y,x,minf)$ %=ev(%, nouns);

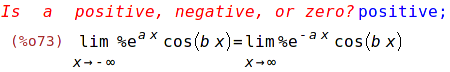
Result

(%i74) assume(a>0);

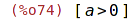
Result

(%i75) 'limit(y,x,minf)$ %=ev(%, nouns);

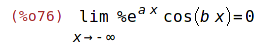
Result

(%i77) facts();

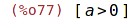
Result

(%i78) forget(a>0);

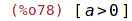
Result

(%i79) facts();

Result

Created with wxMaxima.